

In dieser Einheit werden die Grundlagen einfacher Beleuchtungstechniken erklärt und eingeordnet.
Ziel dieser Einheit soll es sein, zu verstehen, welche Rolle Beleuchtung in der Computergrafik spielt und wie grundlegende Beleuchtungsverfahren funktionieren. Bevor wir uns jedoch genauer mit der Umsetzung beschäftigen, müssen wir uns zunächst erarbeiten, welche Eigenschaften virtuelle Beleuchtung auszeichnen.
Wir wollen uns dafür ein paar Aufnahmen aus verschiedenen Spielen ansehen. Welche Eigenschaften, die ein Beleuchtungsmodell charakterisieren, kannst du daraus ableiten?




Wie auch auf den Screenshots zu erkennen, ist Beleuchtung ein zentrales Ausdrucksmittel und für 3D-Wahrnehmung wichtig. Sie vermittelt Betrachter*innen Informationen über Oberflächenbeschaffenheit und Form von Objekten und trägt dadurch signifikant dazu bei, einen räumlichen Eindruck zu erzeugen.
Um diese Informationen zu vermitteln, muss die Belechtung der Szene also in irgendeiner Form von der Oberfläche abhängen, also insbesondere ihrer Ausrichtung sowie ihrem Material und ihrer Struktur. So würde z.B. ein Ball aus Gummi bei gleicher Beleuchtung anders aussehen als eine Kugel aus Metall.
Dabei sind verschiedene Beleuchtungseffekte zu beobachten: Zum einen sind Flächen stärker erleuchtet, je mehr sie dem Licht zugewandt sind, unabhängig von der Kameraposition. Dieser Bestandteil der Beleuchtung nennt sich diffuse Beleuchtung. Zum anderen sind auch Glanzpunkte zu erkennen, deren Position sich in Abhängigkeit von der Blickrichtung verändert. Diese highlights sind der spekulare Anteil der Beleuchtung.
Wie sich die Stärke der Beleuchtung in Abhängigkeit von z.B. Lichteinfallswinkel und Betrachtungswinkel verhält, kann allgemmein durch Bidirectional Reflectance Distribution Functions (BRDFs) beschrieben werden. In dieser Einheit soll es um eine bestimmte BRDF gehen, welche die Effekte der diffusen und spekularen Beleuchtung einbezieht.
In der Computergrafik I möchten wir zunächst darauf eingehen, wie diese beiden Effekte umgesetzt werden können, um grundlegend plausible Beleuchtung zu erzeugen, die von Oberflächenausrichtung und -material abhängig ist. Natürlich gehört für eine realistische Beleuchtung aber noch einiges mehr dazu. Weiterführende Effekte, die in den Screenshots zu erkennen sind, sind z.B. indirekte Beleuchtung und Schattenwurf.
Direkte vs. Indirekte Beleuchtung
Direkte Beleuchtung bezeichnet alle Beleuchtungseffekte, die nur Licht berücksichtigen, das auf direktem Wege auf die Oberfläche trifft. Unter anderem werden Reflexion oder Refraktion von Licht durch andere Objekte zwischen der Oberfläche und der Lichtquelle nicht berücksichtigt. Wird beispielsweise eine weiße Wand angestrahlt, würde mit einer physikalisch korrekten Darstellung ein Teil des reflektierten Lichts andere Objekte der Szene erleuchten. Dieser Effekt kann durch Beleuchtungsmodelle mit rein direkter Beleuchtung nicht abgebildet werden.
 |
|---|
| Der Einfluss indirekter Beleuchtung ist z.B. an der linken Seite des Quaders zu erkennen. |
Schattierung vs. Schattenwurf
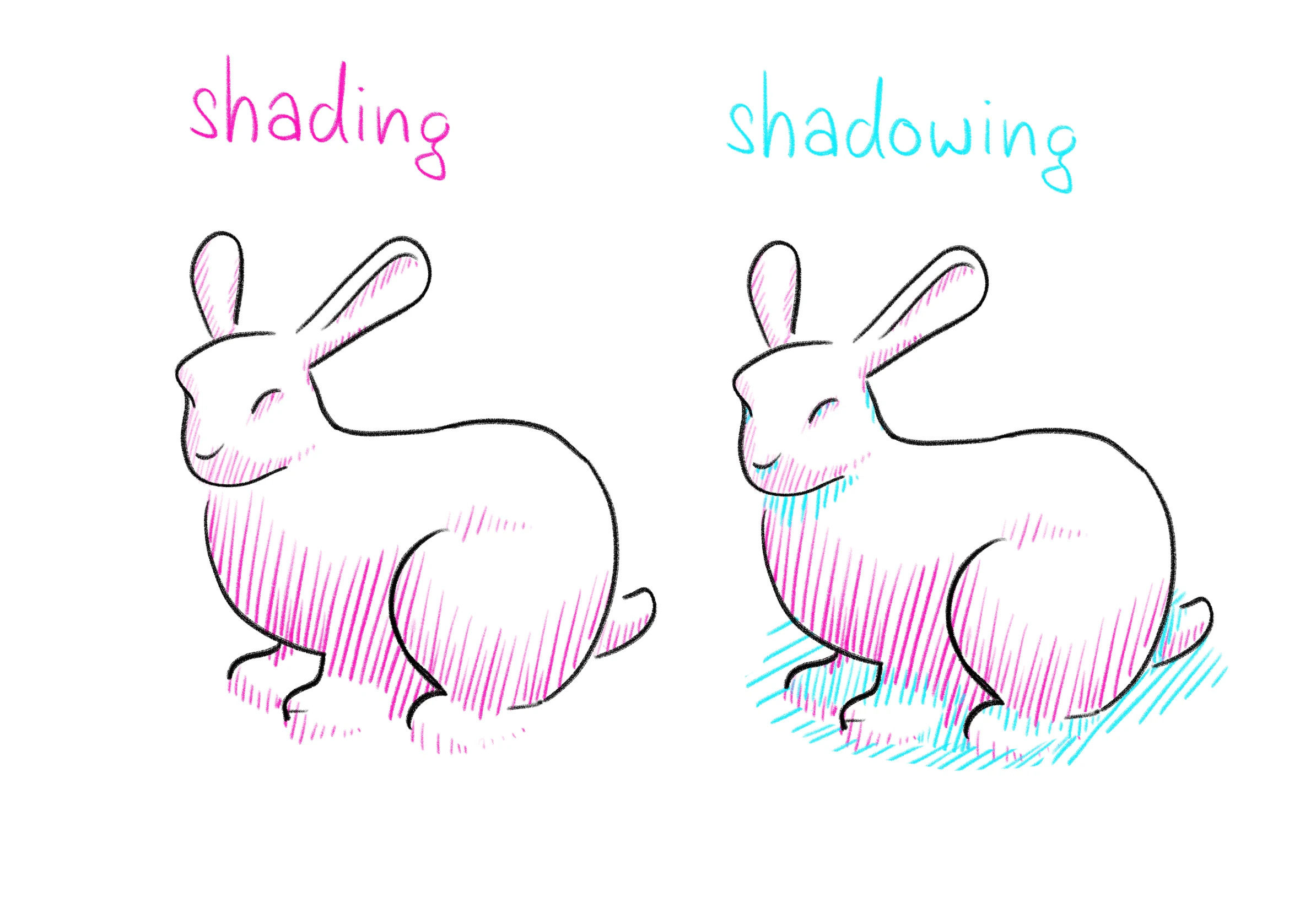
Während es bei der Schattierung darum geht, die Oberflächenfarbe gemäß Material und Ausrichtung gegenüber Lichtquelle und Kamera anzupassen, meint Schattenwurf das Entstehen von Schatten durch Hindernisse zwischen Oberfläche und Lichtquelle.
 |
|---|
| Shading/Shadowing |
Aber was macht diese Effekte so viel schwieriger umzusetzen als direkte Beleuchtung ohne Schattenwurf? Das liegt daran, welche Informationen jeweils benötigt werden, um das Ergebnis zu berechnen. Für direkte Beleuchtung ohne Schatten reicht es aus, die Oberflächennormale und die Positionen von Lichtquellen, Kamera und dem aktuellen Punkt auf der Oberfläche zu kennen. Für indirekte Beleuchtung und Schattenwurf hingegen wird Information über alle Objekte der Szene benötigt, die sich in irgendeiner Weise auf die Beleuchtung der aktuellen Oberfläche auswirken könnten. Zwischen all diesen Objekten kann das Licht zudem potenziell beliebig oft hin und her reflektiert werden, was die Beleuchtungsberechnung deutlich komplexer und rechenintensiver macht.
Es gibt natürlich viele clevere Ansätze, um auch mit weniger Rechenkapazität einige Aspekte komplexerer Beleuchtung umzusetzen. Einige davon, insbesondere Techniken zum Annähern von Schatten, werden in Computergrafik II thematisiert.
Zusammenfassung:
Für eine detailliertere Einführung in die physikalischen Grundlagen des Lichts empfehlen wir die Seite von Bartosz Ciechanowski. Für diese Einheit werden wir jedoch ein einfaches Strahlenmodell annehmen.
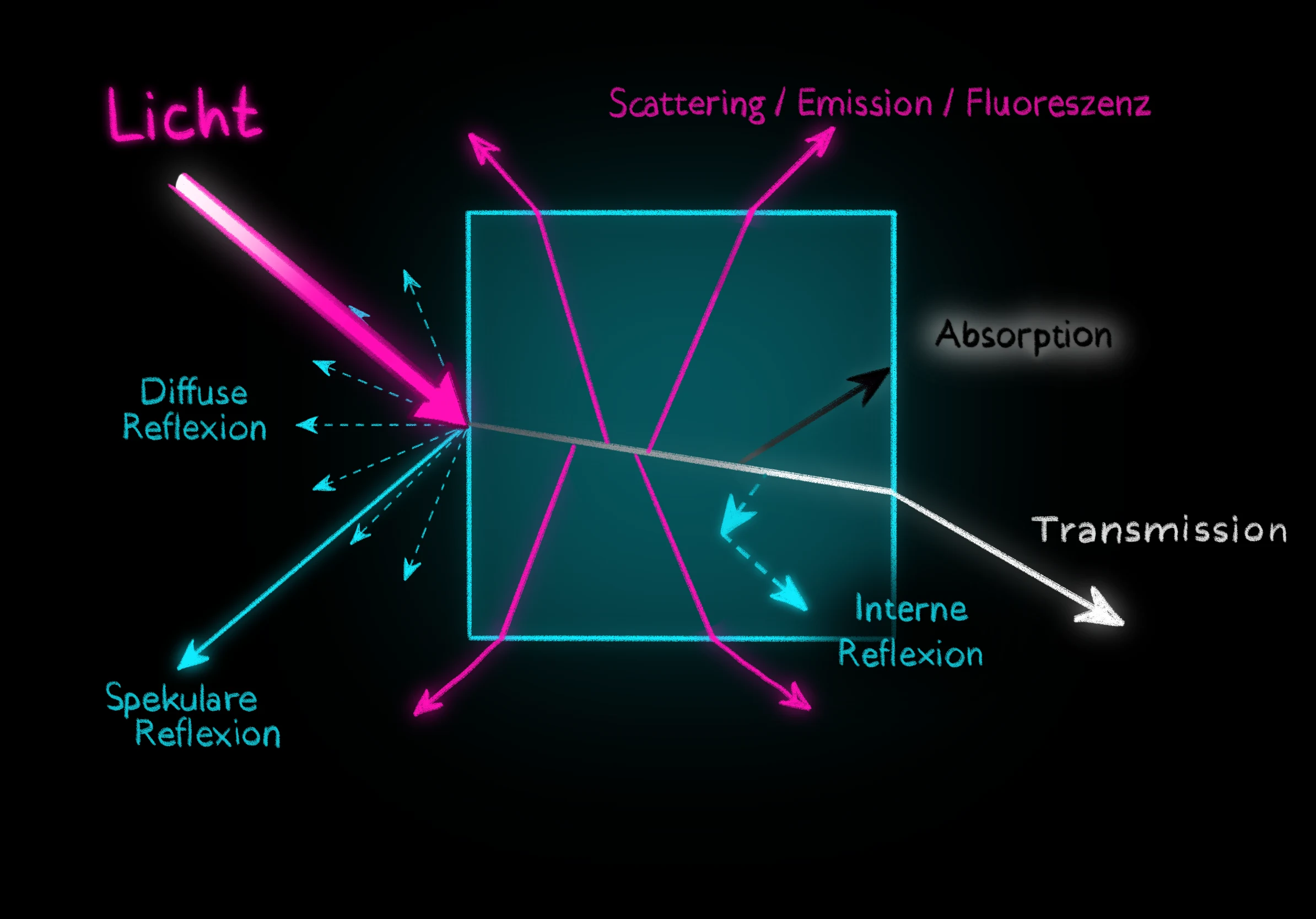
Wir nehmen die Welt um uns darüber wahr, wie Licht mit ihr interagiert. Wir können Objekte nur sehen, wenn sie mit Licht in Kontakt kommen und dieses entweder in Richtung Betrachter*in zurückwerfen (Reflexion), durchlassen (Transmission) oder verschlucken (Absorption). Diese Erscheinungen nehmen Einfluss darauf, wie hell oder dunkel ein Objekt wahrgenommen wird, und bewirken dadurch Schattierung und Schattenwurf. Damit bilden sie auch die Grundlage für unser Beleuchtungsmodell.
Alle Bestandteile dieses Modells sind im folgenden beispielhaft illustriert.
 |
|---|
Weitere Phänomene, die bei der Interaktion von Licht mit Objekten einer Szene auftreten können, sind z.B. Lichtbeugung und -brechung sowie Interferenzerscheinungen -- diese spielen jedoch in den Lichtausbreitungsmodellen der Computergrafik in der Regel eine untergeordnete Rolle. Den Hauptfaktor bildet die Reflexion.
Im Folgenden werden wir die Intuition hinter den Hauptbestandteilen des Phong-Beleuchtungsmodells erarbeiten.
Wie bereits erwähnt unterscheiden wir zwischen diffuser und spekularer Reflexion, die zusammen unser (sehr simples) Beleuchtungsmodell bilden. Welche physikalischen Grundlagen bzw. welche Modellannahmen stecken dahinter?
Als diffuse Reflexion wird der Effekt bezeichnet, dass Flächen heller wirken, je mehr sie dem Licht zugewandt sind. Sie ist vollständig unabhängig vom Betrachtungswinkel und nur von Oberflächenausrichtung und Lichtposition bzw. Lichtrichtung abhängig.
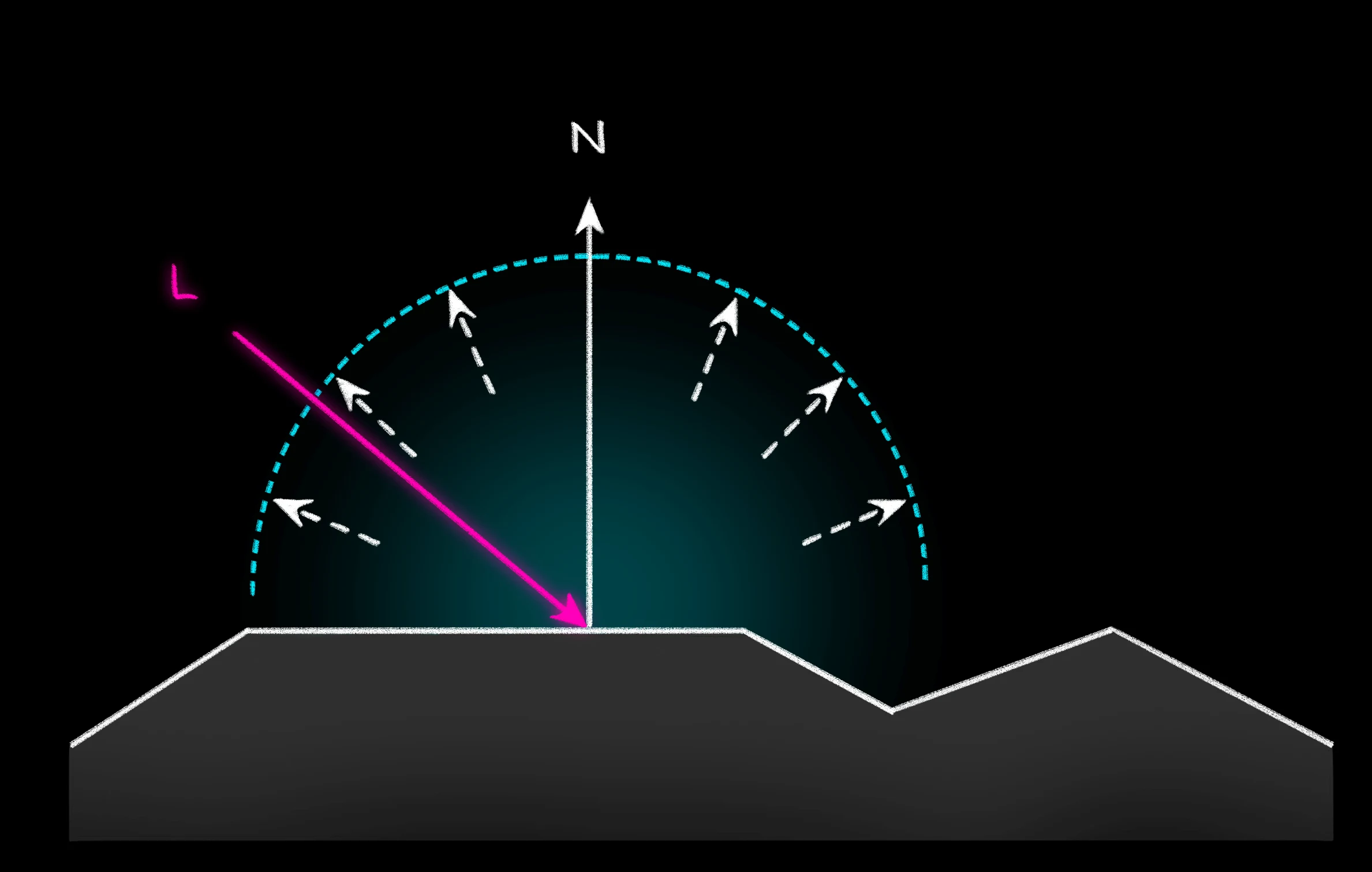
Es steht die Modellannahme dahinter, dass das auf die Oberfläche auftreffende Licht gleichmäßig in alle Richtungen reflektiert wird. Dieses Phänomen ist stärker, je rauer die Oberfläche ist.
 |
|---|
| Diffuse Reflexion - modelliertes Verhalten |
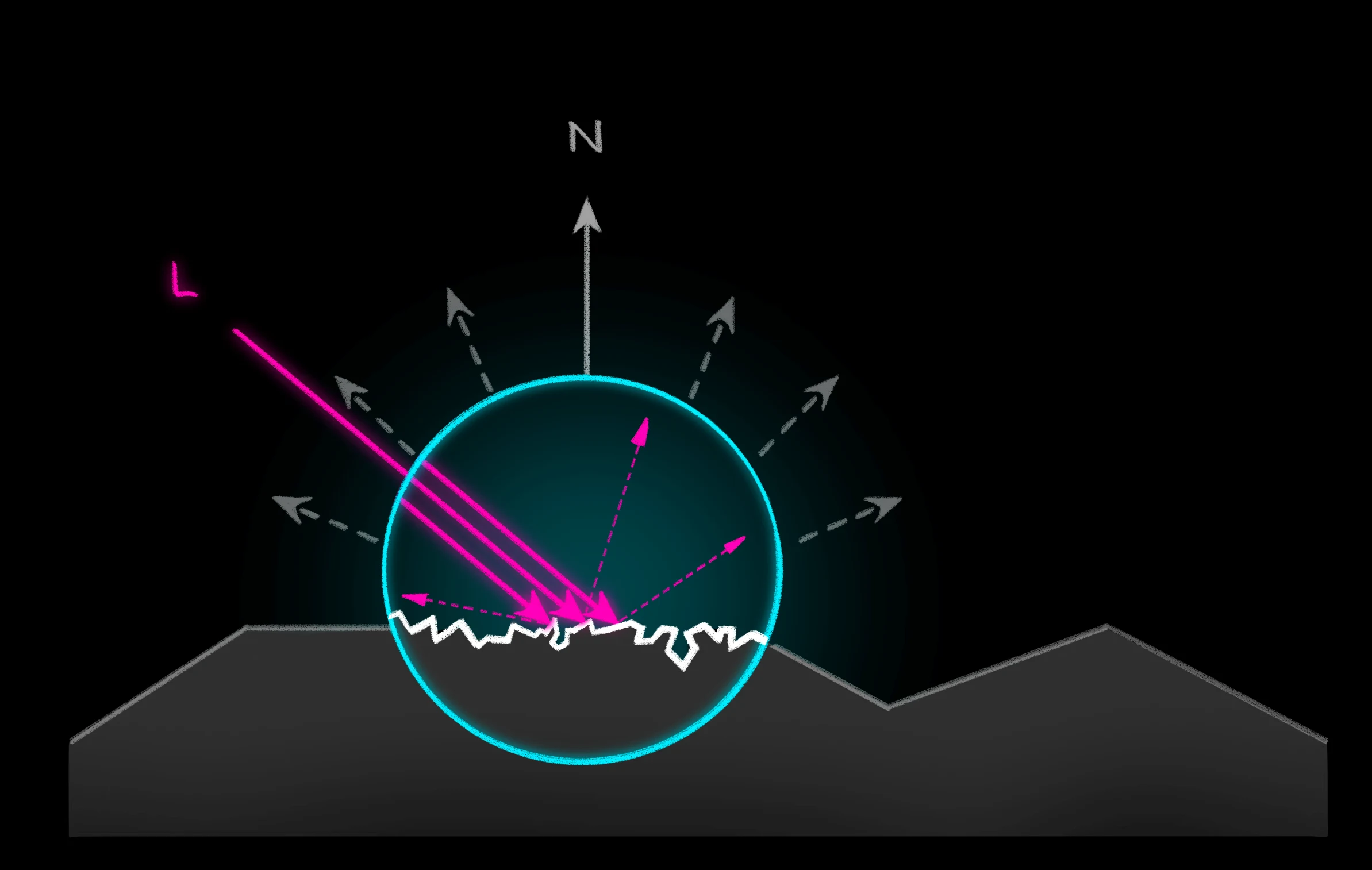
Physikalisch lässt sich dieses Phänomen damit begründen, dass raue Flächen viele kleine Unebenheiten beinhalten. Wir können uns die Wirkung einer Lichtquelle als viele dicht nebeneinanderliegende Lichtstrahlen vorstellen. Treffen diese auf die Fläche, werden sie in praktisch zufällige Richtungen reflektiert. Durch dieses Verhalten der einzelnen Lichtstrahlen wird das Licht insgesamt annähernd gleichmäßig (isotrop) in alle verschiedenen Richtungen reflektiert.
 |
|---|
| Reflexion an Unebenheiten in der Oberfläche |
Wie viel Licht genau in Abhängigkeit vom Lichteinfallswinkel reflektiert wird, lässt sich mithilfe des Lambertschen Gesetzes berechnen. Dieses besagt, dass die reflektierte Lichtmenge, also die Lichtintensität
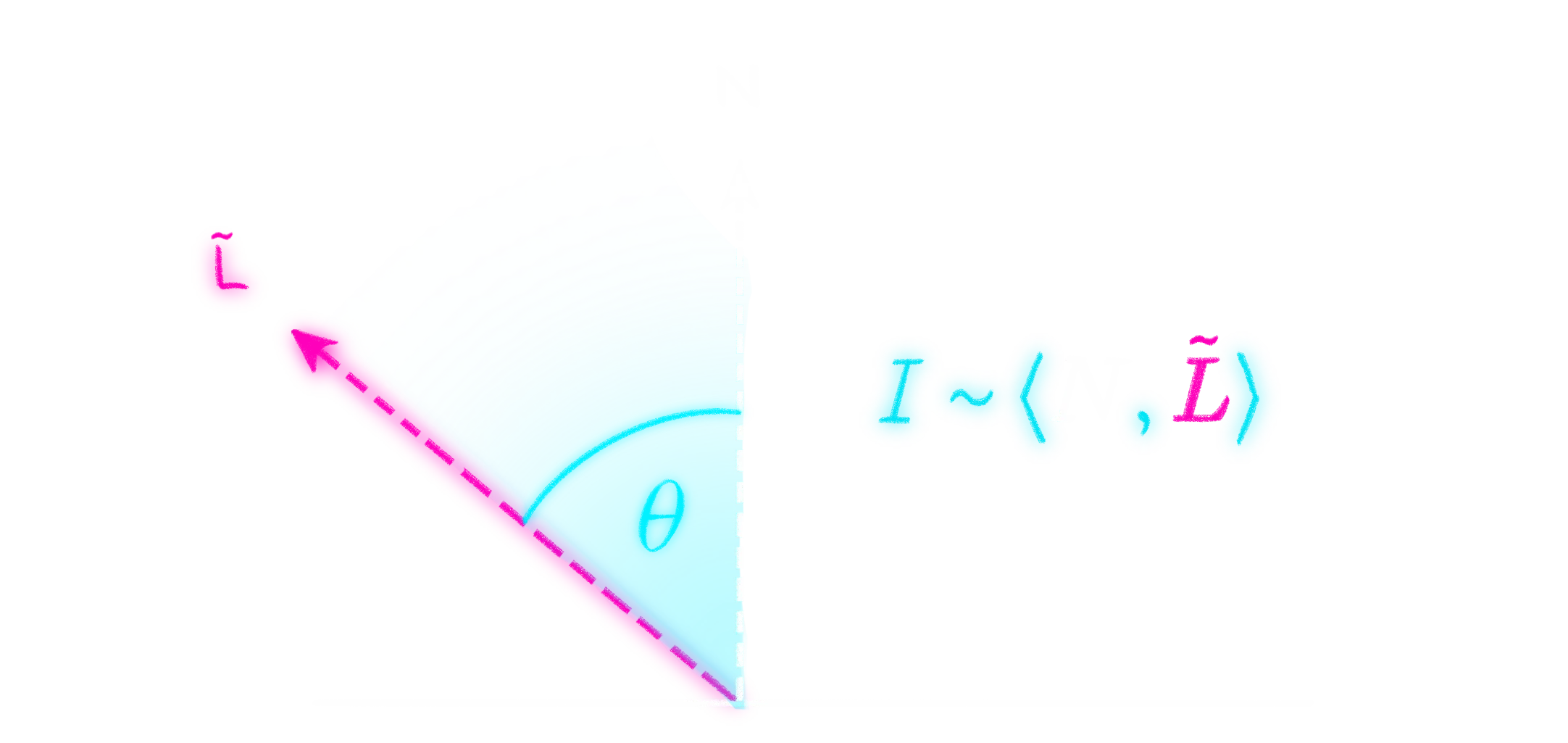 |
|---|
| Lambertsches Gesetz |
Dieser Zusammenhang lässt sich auch aus folgender Überlegung über das Strahlenmodell herleiten. Wir können uns das Licht als ein Bündel paralleler Lichtstrahlen mit gleichem Abstand vorstellen. Je größer der Winkel der Lichtstrahlen zur Flächennormale ist, umso größer ist der Abstand, mit dem die Lichtstrahlen auf der Oberfläche aufkommen. Die gleiche Fläche wird also bei einem größeren Winkel von weniger Lichtstrahlen getroffen.

Mit dieser Intuition können wir nun auch die Abhängigkeit vom Skalarprodukt zwischen Lichtrichtung und Normale erklären:
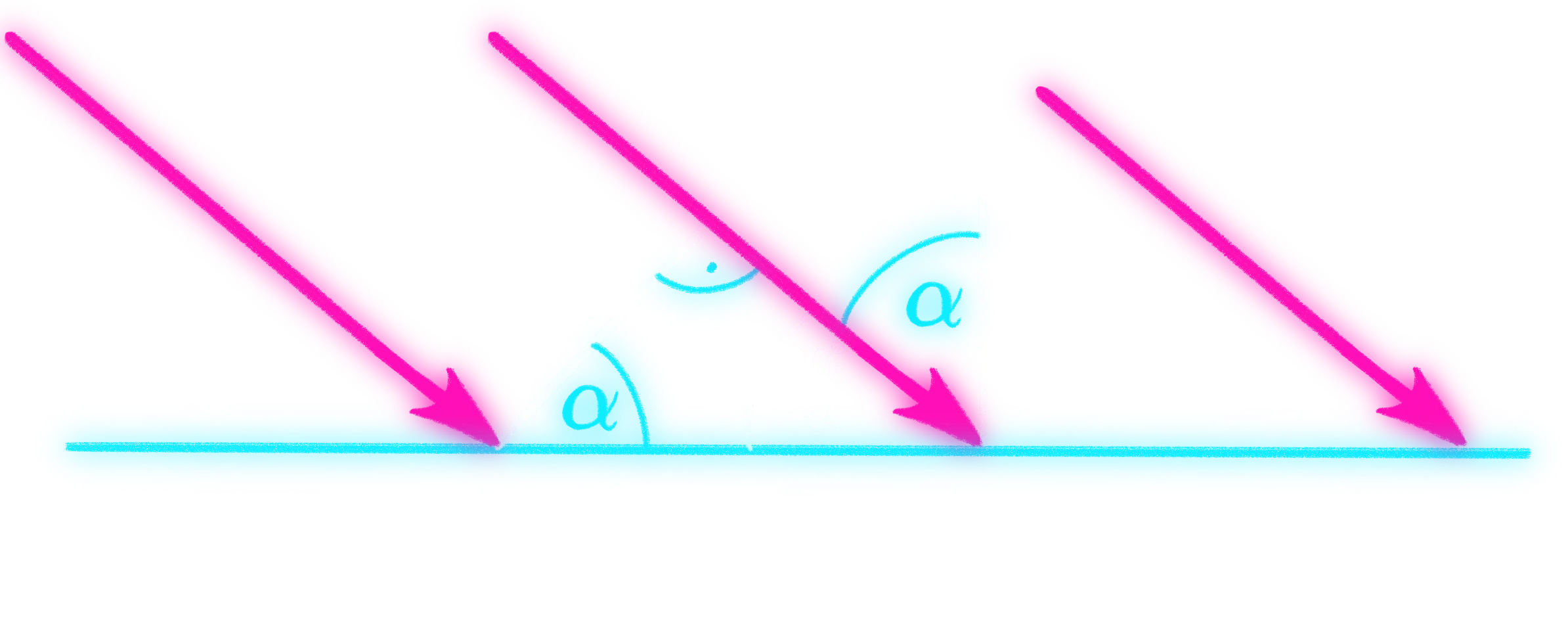 |
|---|
Je größer der Abstand
Damit können wir also die Abhängigkeit der diffusen Reflexion von sowohl der Oberflächenbeschaffenheit als auch von der Lichtrichtung begründen.
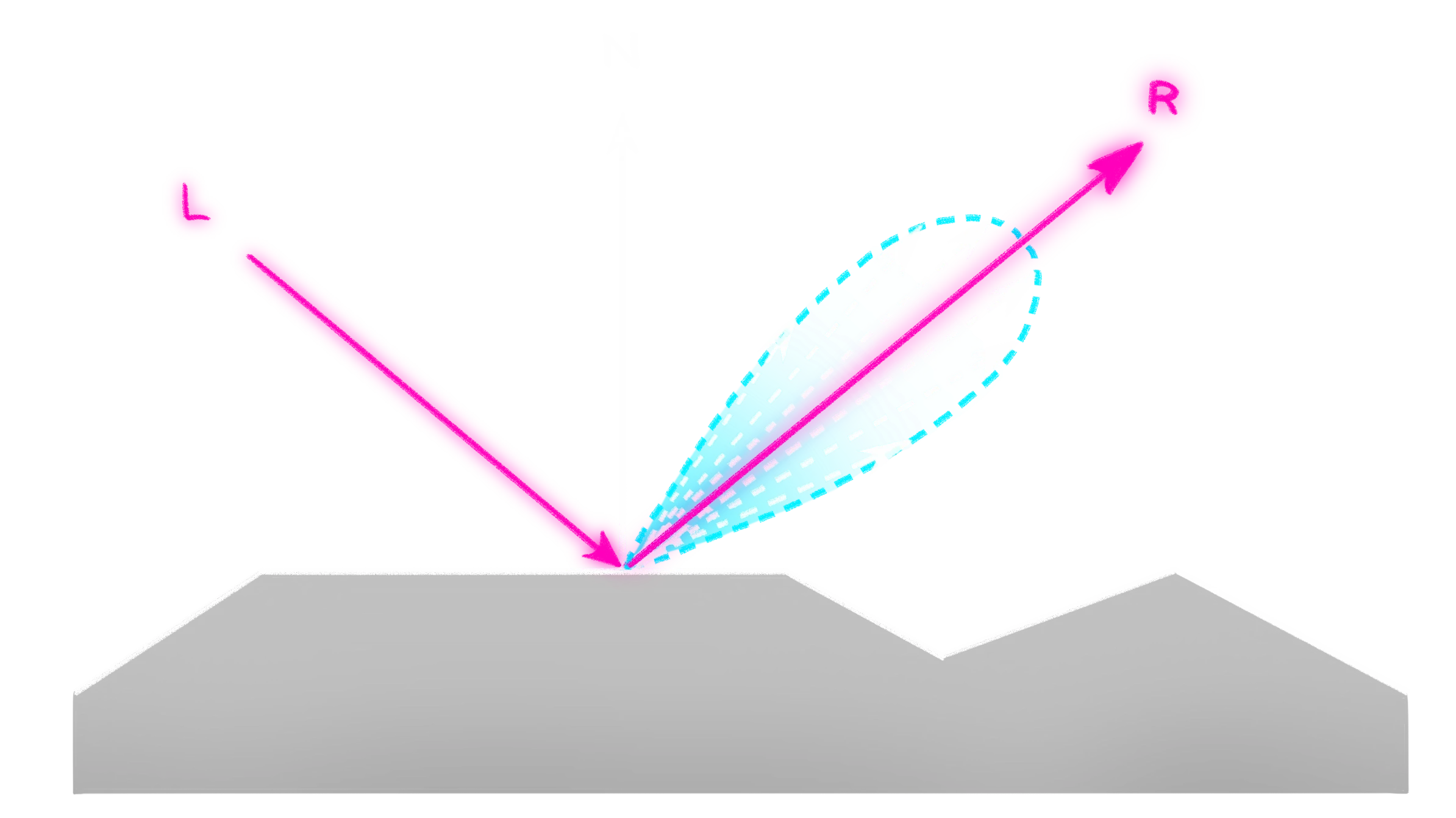 |
|---|
| Spekulare Reflexion -- modelliertes Verhalten |
Im Gegensatz zur Diffusen Reflexion ist die Spekulare Reflexion (auch spiegelnde Reflexion oder Spiegellicht) nicht nur von der Oberflächenbeschaffenheit und Lichtrichtung, sondern auch der Blickrichtung abhängig.
Hier ist die Modellannahme, dass sich das Licht (im Gegensatz zur gleichmäßigen diffusen Reflexion) ungleichmäßig und besonders konzentriert in eine Richtung
Spekulare Reflexion ist stärker auf sehr glatten (z.B. polierten) Oberflächen. Die Oberflächenbeschaffenheit bestimmt dabei sowohl, wie stark die spekulare Reflexion ist, als auch wie schnell die Helligkeit mit zunehmender Abweichung zwischen Blick- und Spiegelrichtung abnimmt.
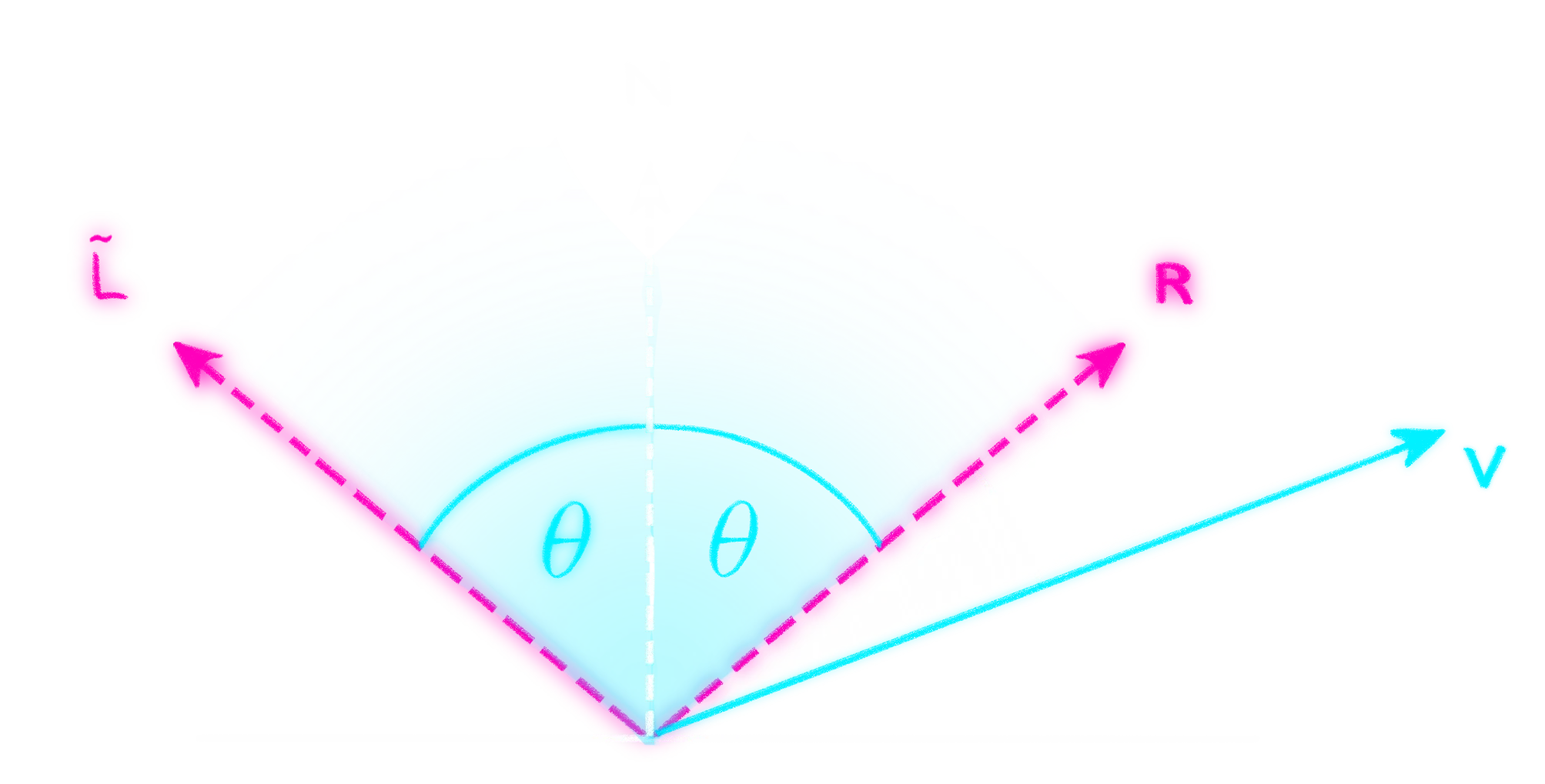 |
|---|
| Spekulare Reflexion |
Sei
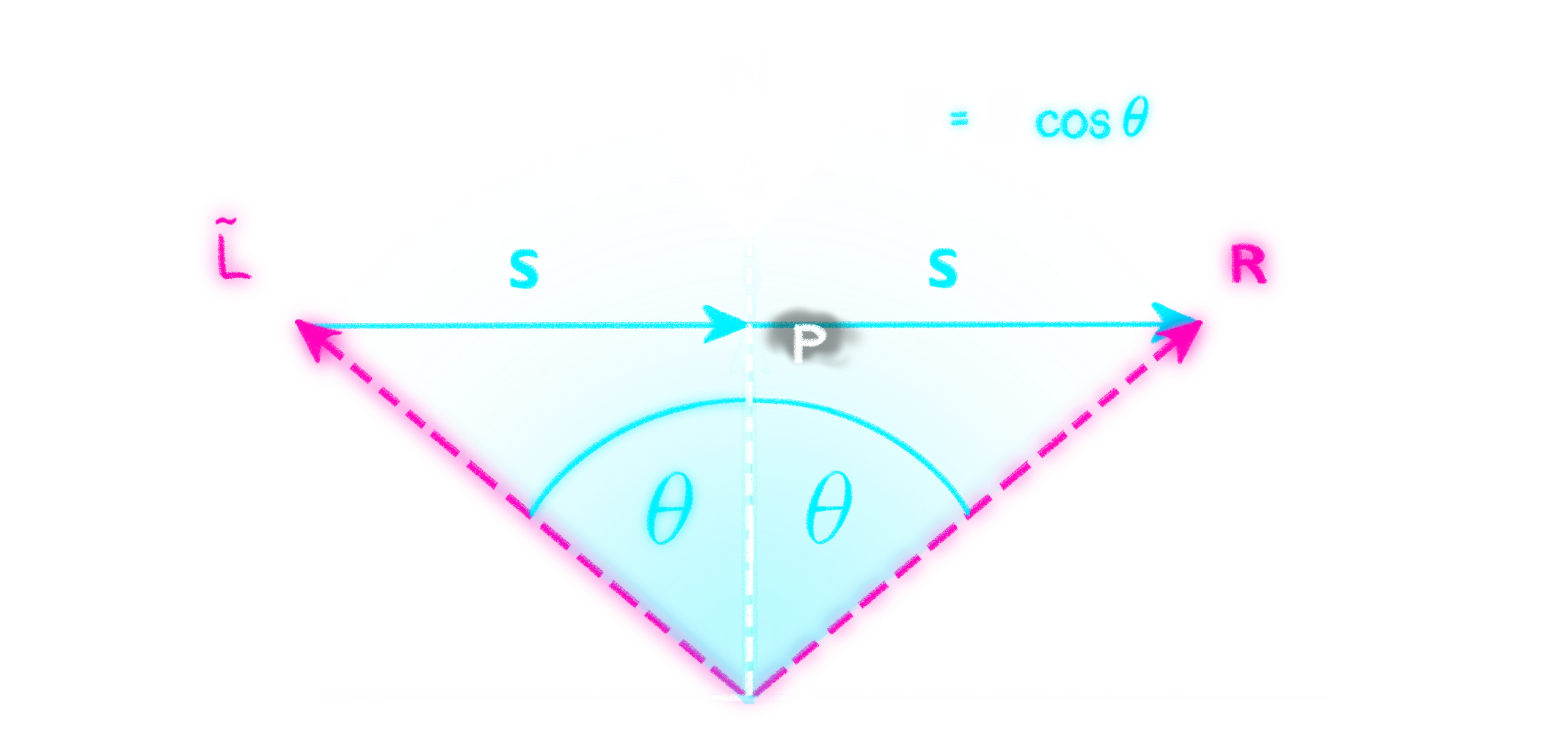 |
|---|
| Berechnung der Spiegelrichtung |
Die Spiegelrichtung
Sei
Wie auch in der Abbildung gut erkennbar ist, entspricht der Reflexionsvektor
Diese Überlegungen bilden die Theorie hinter grundlegenden Beleuchtungstechniken. Für die Implementierung sind noch weitere Aspekte zu beachten, die wir im folgenden beleuchten wollen.
Bisher war lediglich von Lichtintensitäten die Rede – doch wenn wir Objekte nicht nur in Graustufen darstellen wollen, benötigen wir eine Möglichkeit um aus Licht- und Objektfarbe sowie Intensitätsinformationen die resultierende sichtbare Farbe zu bestimmen. Klassischerweise werden die Lichtintensität, die Objektfarbe und die Lichtfarbe durch Multiplikation zur resultierenden Gesamtfarbe kombiniert.
Die bisherige Berechnung der spekularen Reflexion im Phong-Beleuchtungsmodell ist vergleichsweise intuitiv, da direkt der Zusammenhang zwischen dem Winkel zwischen Reflexions- und Blickrichtung klar ist. Sie besitzt jedoch zum einen den Nachteil, dass sie relativ komplexe Berechnungen benötigt - allein um den Reflexionswinkel zu bestimmen, müssen zwei Skalarprodukte berechnet werden. Zum anderen weichen die Ergebnisse teils noch von realitätsgetreuen Bildern ab.
Eine Technik, die diese Probleme adressiert, ist Blinn-Phong-Beleuchtung. Hier wird die spekulare Beleuchtung anders berechet: Statt jedes Mal den Reflexionsvektor zu bestimmen, um anschließend den Winkel zur Blickrichtung zu berechnen, wird stattdessen ein sogenannter Half-Vector
In der folgenden Demo wird visualisiert, wie für verschiedene Licht- und Blickrichtungen in beiden Varianten der entsprechende Winkel und die daraus resultierende Helligkeit aussehen.
Es ist zu erkennen, dass der Winkel bei Blinn-Phong immer halb so groß ist wie im Phong-Modell. Wer möchte, kann diesen Zusammenhang gerne für sich als Übung beweisen.
Die folgende Demo zeigt den Unterschied zwischen Phong-Beleuchtung und Blinn-Phong-Beleuchtung am Beispiel einer von drei verschiedenen Lichtquellen beleuchteten Kugel. Mit dem Slider kann zwischen Phong (links) und Blinn-Phong (rechts) gewechselt werden. Zu beachten ist, dass bei Blinn-Phong ein höherer Spekularitäts-Exponent verwendet wurde, um die Ergebnisse anzugleichen.
Mit diesen Überlegungen haben wir die Grundlagen des Phong-Beleuchtungsmodells hergeleitet. Dieses ist verhältnismäßig eingeschränkt und in den Ergebnissen kaum realistisch, weshalb es heutzutage auch im Real-Time-Rendering größtenteils von anderen Modellen abgelöst wurde. Viele davon basieren auf der Idee von Physically Based Rendering (PBR). Dieses hat zum Ziel, Beleuchtung basierend auf realweltlichen Oberflächeneigenschaften (z.B. metalness oder roughness) möglichst realistisch zu modellieren.
Die Ideen des Phong-Beleuchtungsmodells sind aber auch in den moderneren Ansätzen wiederzufinden -- damit bietet es einen guten Einstieg, um grundlegende Konzepte von Echtzeit-Beleuchtungsmodellen zu verstehen.